Annexe B Analyses factorielles et Analyses en facteurs communs
Les parties B.1 et B.2 correspondent à une synthèse de Juhel (2019), la partie B.3.1 à une synthèse de la documentation Wikipédia de l’ACM et la partie B.3.3 de Fabrigar, Wegener, MacCallum, & Strahan (1999).
B.1 Analyse en facteurs communs exploratoire (AFE)
B.1.1 Philosophie et genèse de l’analyse en facteurs commun
L’analyse en facteurs communs (AF) fait partie des méthodes multivariées les plus anciennes dont le développement a été impulsé par des chercheurs en psychologie. L’AF repose en effet initialement sur l’hypothèse que les différences psychologiques observables et mesurées entre individus (typiquement réponses à un test mental) reflètent des sources communes de variation, elles non observables, appelées facteurs communs ou variables latentes. C’est une approche philosophique différente des méthodes d’analyse factorielle plus connues en France (voir partie B.3) telles que l’Analyse en Composantes Principales (ACP, Hotelling (1933)) et ses petites sœurs adaptées aux variables quantitatives, notamment l’Analyse Factorielle des Correspondances (Benzécri (1982)) de laquelle découle l’Analyse en Correspondances Multiples (ACM).
Spearman (1904) est un article fondateur pour ces théories. Il fait l’hypothèse que la performance \(Y_j\) est le résultat de deux sources de variations : \(Y_j = a_j g + S_j\).
une « fonction fondamentale commune (ou groupe de fonctions) » appelée \(g\) ;
un facteur \(S_j\) spécifique au test.
Cette intuition de Spearman est d’ordre psychologique et est peu basée sur la théorie statistique. C’est pourquoi les recherches ultérieures eurent du mal à retrouver la structure factorielle qu’il avait conjecturée. L. L. Thurstone (1935) introduisit davantage de mathématiques dans la théorie de Spearman en supposant l’existence de non pas un mais plusieurs facteurs de groupes (comme le fera aussi Burt (1941)), sans pour autant faire d’hypothèse sur la nature de ces derniers (innée, acquis…), ce qui élargira finalement l’utilisation de ces méthodes à des domaines différents de la psychologie. L. L. Thurstone (1935) montre que le nombre de facteurs communs se déduit de la matrice de corrélation. Il introduit également le concept de communauté, ou de variance commune (voir figure B.1) qui résume la proportion de variance qu’un test a en commun avec les autres tests. Il développe aussi la méthode centroïde d’extraction des facteurs qui utilise notamment une méthode de rotation de facteurs (voir partie B.1.3.3) mettant ainsi un point d’honneur à l’analyse des résultats obtenus (caractère exploratoire et non confirmatoire).
B.1.2 Formalisation mathématique
Une AF se définit par un système (équation (B.1)) qui comporte autant d’équations linéaires que de variables observées (\(p\) variables observées associées à \(p\) facteurs uniques) appliquées aux \(n\) individus. Chaque variable observée est une fonction linéaire de \(m\) facteurs communs (variables inobservables et latentes qui influencent des variables mesurées et tiennent compte de leurs corrélations) et d’un facteur unique (variable latente qui influence une unique variable mesurée). Ce facteur unique se décompose en une composante spécifique et éventuellement une erreur de mesure.
De la même manière, la variance totale se décompose en une somme de deux variances (cf. figure B.1) :
la variance commune (communauté ou communality) qui correspond à la variance partagée par tous les indicateurs d’un même facteur ;
la variance unique (inexistante dans le cas d’une ACM) : celle spécifique à chaque indicateur (par exemple la variance spécifique du fait de toucher le RSA au-delà de la variance attribuable à la pauvreté institutionnelle) et celle due aux éventuelles erreurs de mesure.
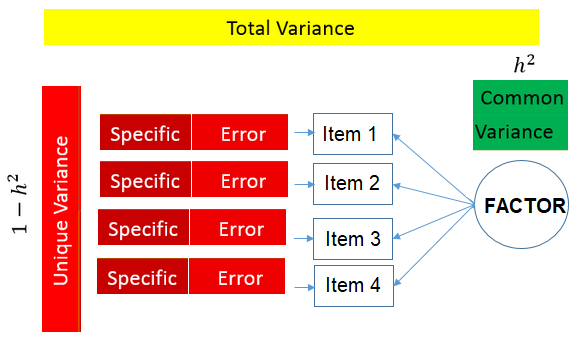
Figure B.1: Décomposition de la variance
inspiré du tutoriel de l’UCLA A Practical Introduction to Factor Analysis: Exploratory Factor Analysis
L’objectif est alors de comprendre la structure des corrélations entre variables mesurées en estimant les relations entre chaque variable mesurée et les facteurs communs. Mathématiquement :
\[\begin{equation} Y = \Lambda F + \Psi E \tag{B.1} \end{equation}\]
Avec :
- \(F[n, m]\) la matrice des scores aux \(m\) facteurs communs ;
- \(\Lambda [p, m]\) la matrice de saturation (en anglais loadings) dont chaque élément représente l’influence linéaire d’un facteur commun sur une variable observée ;
- \(E[n, p]\) la matrice des scores aux \(p\) facteurs uniques ;
- \(\Psi [p, p]\) la matrice diagonale des variances uniques des variables observées (définies positives).
Comme le nombre de variables inconnues (les \(m\) facteurs communs et \(p\) facteurs uniques) est supérieur au nombre de variables connues (\(p\) variables observées), le modèle est indéterminé. Différentes hypothèses supplémentaires sont nécessaires pour obtenir une formule pour la matrice de corrélations \(R\) (équation (B.2)) :
- les moyennes des facteurs communs et uniques sont nulles
- les facteurs communs ne sont pas corrélés aux facteurs uniques
- les facteurs uniques ne sont pas mutuellement corrélés.
L’équation fondamentale de l’AF s’écrit alors (Mulaik (2009)) :
\[\begin{equation} R = \Lambda \Phi \Lambda' + \Psi^2 \tag{B.2} \end{equation}\]
Avec :
- \(R[p, n]\) la matrice de corrélation des \(p\) variables observées ;
- \(\Phi [p, p]\) la matrice de corrélation entre facteurs communs.
Si l’on suppose que les facteurs communs sont orthogonaux, alors \(\Phi=I_p\) et les \(\Lambda\Lambda'\) correspondent aux communautés des variables observées et on a :
\[\begin{equation} R = \Lambda \Lambda' + \Psi^2 \tag{B.3} \end{equation}\]
Par ailleurs, pour que le modèle soit bien déterminé, on doit avoir un nombre minimal d’indicateurs \(p\) dans notre modèle : \(p > \frac{1}{2} [ (2m + 1) + \sqrt{8m + 1} ]\) (Ledermann (1937)). C’est-à-dire au moins 3 variables pour 1 facteur, 5 variables pour 2 facteurs, 6 variables pour 3 facteurs, etc.
B.1.3 Mise en œuvre de l’AFE
B.1.3.1 Extraction des facteurs communs
Les paramètres du modèle à estimer à partir des données observées correspondent aux \(pm\) saturations des variables observées sur les \(m\) facteurs et aux \(p\) variances uniques des variables observées, soient en tout \(p(m+1)\) paramètres27.
La méthode d’extraction la plus connue est algébrique (et non statistique). Il s’agit de l’analyse en axes principaux avec estimation des communautés initiales (PAF : iterated Principal Axis Factoring). Cette méthode est conditionnelle aux estimations a priori des communautés et est basée sur l’ACP (Hotelling (1933)) de la matrice de corrélation réduite \(R^* = R - \Psi^2\). Elle présente les avantages de ne nécessiter aucune hypothèse sur la distribution des variables observées, de pouvoir être employée quand la matrice de corrélation n’est pas régulière, de rencontrer moins de problèmes de convergence que des méthodes statistiques et de ne pas conduire à des « cas Heywood » (variances uniques négatives).
A partir des années 1960, l’accroissement de la puissance de calcul computationnel rend possible une estimation plus rigoureuse des saturations et des variances uniques. Divers algorithmes d’estimation, désormais statistiques, sont développés pour trouver les valeurs de \(\Lambda\) et de \(\Psi^2\). Ils sont techniquement complexes mais faciles à mettre en œuvre dans la pratique pour estimer les paramètres d’une AFE. En particulier, Jöreskog (1967) propose un modèle statistique aléatoire accompagné d’une procédure d’optimisation numérique permettant l’estimation du maximum de vraisemblance28 des paramètres du modèle en facteurs communs.
\[\begin{equation} y = \Lambda f + e \tag{B.4} \end{equation}\]
Avec :
- \(y[p, 1]\) un vecteur aléatoire de \(p\) variables observées de moyenne \(\mu=0\) et de matrice de covariance \(\Sigma\) sur la population ;
- \(f [m, 1]\) un vecteur aléatoire de \(m \leq p-1\) facteurs communs ;
- \(\Lambda [p, m]\) une matrice des saturations des \(p\) variables observées sur les \(m\) facteurs ;
- \(E[p, 1]\) un vecteur aléatoire des variances uniques des \(p\) variables observées.
Avec les hypothèses supplémentaires suivantes :
- \(E(f) = E(e) = E(fe') = 0\)
- \(E(ee') = \Psi^2\)
Et si \(E(ff') = I_m\), alors on retrouve :
\[\begin{equation} \Sigma = \Lambda \Lambda' + \Psi^2 \tag{B.5} \end{equation}\]
Le modèle factoriel représente maintenant l’hypothèse statistique testable que la matrice de covariance de la population a la structure impliquée par l’équation (B.5) pour un nombre prescrit \(m\) de facteurs. Il s’agit alors, si l’on suppose correcte l’équation fondamentale de l’AF sur la population, de trouver les meilleures estimations au sens du maximum de vraisemblance qui minimisent la distance entre la matrice de covariance observée \(S\) et la matrice de covariance \(\hat \Sigma = \hat{\Lambda}_m \hat{\Lambda}_m' + \hat {\Psi}^2\) impliquée par le modèle en facteurs communs où \(\hat{\Lambda}_m\) et \(\hat {\Psi}^2\) sont les estimations des valeurs « vraies » de \(\Lambda_m\) et \(\Psi^2\) dans la population.
B.1.3.2 La détermination du nombre de facteurs communs
Il faut ensuite déterminer le nombre de facteurs communs nécessaires pour obtenir une matrice de saturation reconstruisant le mieux possible la matrice de corrélation entre variables observées (équation (B.3)). Comme pour l’analyse en composantes principales, de nombreuses règles et procédures existent pour déterminer le nombre optimal de facteurs. Cette procédure est, en outre, ici d’autant plus importante que le nombre de facteurs choisis modifie les résultats obtenus alors que, dans une ACP, ce choix n’influe qu’au moment d’effectuer une interprétation des résultats puisqu’il est fait a posteriori. C’est pourquoi il est recommandé de s’appuyer sur plusieurs critères. En voici deux basés sur les valeurs propres de la matrice de corrélations :
La règle de Kaiser-Guttman consiste à extraire un nombre de facteurs égal au nombre de valeurs propres supérieures ou égales à 1 (Guttman (1954); Kaiser (1960)).
Appliquée à la matrice de corrélation réduite, la version graphique ou numérique du scree-test de Cattell (1966) est employée pour déterminer une rupture de pente dans la courbe des valeurs propres à partir de laquelle la variance restante est jugée de faible importance ; le nombre de facteurs à extraire est alors donné par le nombre de valeurs propres supérieures à la valeur du point de rupture.
B.1.3.3 La rotation de la structure factorielle initiale
La structure orthogonale initiale (équation (B.4)) n’est qu’une représentation parmi une infinité de solutions factorielles qui permettent de reconstruire les corrélations du modèle étudié. C’est pourquoi cette structure initiale est habituellement transformée en appliquant une rotation – orthogonale ou oblique – à la matrice de saturation afin d’obtenir une structure simple plus facilement interprétable sans pour autant changer l’estimation du modèle29.
Les premières méthodes de rotation utilisées par L. Thurstone (1947) étaient géométriques. Elles étaient non seulement chronophages lorsque le nombre de facteurs (et donc de plans) étaient élevés mais on leur reprochait également d’être guidées par l’intuition des analystes et non par des hypothèses explicites.
Les méthodes analytiques de rotation qui apparurent par la suite reposent sur des principes formels indépendants du contenu des variables et visent à mieux faire apparaître les saturations élevées ou « saillantes » des variables sur les facteurs. Le modèle factoriel exploratoire le plus restreint fait l’hypothèse de corrélations nulles entre facteurs (rotation orthogonale), plusieurs variantes de ce type existent : Varimax, Quartimax, Parsimax, Orthomax. Une représentation plus plausible de la réalité et généralement recommandée est fournie par le modèle factoriel exploratoire non restreint qui fait l’hypothèse de facteurs corrélés (rotation oblique). Ses différentes variantes sont encore plus nombreuses : Quartimin, Promax, Orthoblique, Orthomin, Direct Oblimin, Geomin, Promaj, Promin, etc.
B.2 Analyse en facteurs communs confirmatoire (AFC)
L’Analyse en facteurs communs confirmatoire (AFC30 ; Jöreskog (1969) et Jöreskog (1971)) cherche comme l’AFE à reproduire les relations entre des variables observées avec un plus petit nombre de facteurs mais les deux méthodes diffèrent dans leur philosophie. Alors que l’objectif de l’AFE est de déterminer le nombre de facteurs communs, corrélés ou pas par hypothèse, et d’identifier des indicateurs notoires des facteurs parmi les variables observées (approche data-driven), celui de l’AF confirmatoire est de tester empiriquement l’hypothèse d’une structure factorielle prédéfinie par le chercheur. Le cadre théorique doit donc être suffisamment explicite pour pouvoir incorporer des hypothèses structurales dans la spécification et l’estimation du modèle afin de tester celles-ci directement.
Il est parfois utile de mobiliser AFE et AFC dans une même recherche. En pratique, on utilise souvent une AFE avec rotation oblique avant une AFC pour voir si les hypothèses structurales théoriques que l’on formule se confirment bien empiriquement. On peut également utiliser une AFE sur une première moitié de l’échantillon pour spécifier un modèle confirmatoire que l’on estime sur la deuxième partie de l’échantillon par une AFC.
Le modèle de l’AF confirmatoire est le même que celui de l’AF exploratoire en facteurs obliques. On considère toujours \(m\) facteurs communs (dont on fixe cette fois-ci le nombre) pour lesquels il faut estimer la matrice de saturation \(\Lambda\).
\[\begin{equation} \Sigma = \Lambda \Phi \Lambda' + \Theta \tag{B.6} \end{equation}\]
Avec :
- \(\Sigma [p, p]\) la matrice de covariance des \(p\) variables observées ;
- \(\Lambda [p, m]\) la matrice creuse31 de saturation des \(p\) variables observées sur les \(m\) facteurs ;
- \(\Phi[p, p]\) la matrice de covariance entre facteurs communs (qui peuvent ou non être corrélés) ;
- \(\Theta [p, p]\) la matrice de covariance des erreurs des \(p\) variables observées32.
À ces restrictions structurales, dont le bien-fondé peut être testé, s’ajoutent des contraintes d’identification du modèle qui sont nécessaires pour obtenir une solution unique. La métrique des facteurs est identifiée en imposant \(m\), par exemple en fixant une saturation par facteur à une constante non nulle (1 en général) ou en fixant à 1 les variances des facteurs comme dans l’AF exploratoire. L’indétermination de la rotation est résolue en imposant au moins \(m(m-1)\) contraintes, par exemple en libérant les éléments sous-diagonaux de \(\Phi\) et en fixant \((m-1)\) saturations à 0 par facteur. Le nombre de contraintes d’identification et de restrictions structurales est donc plus élevé dans l’AF confirmatoire que dans l’AF exploratoire (cf. figure B.2).
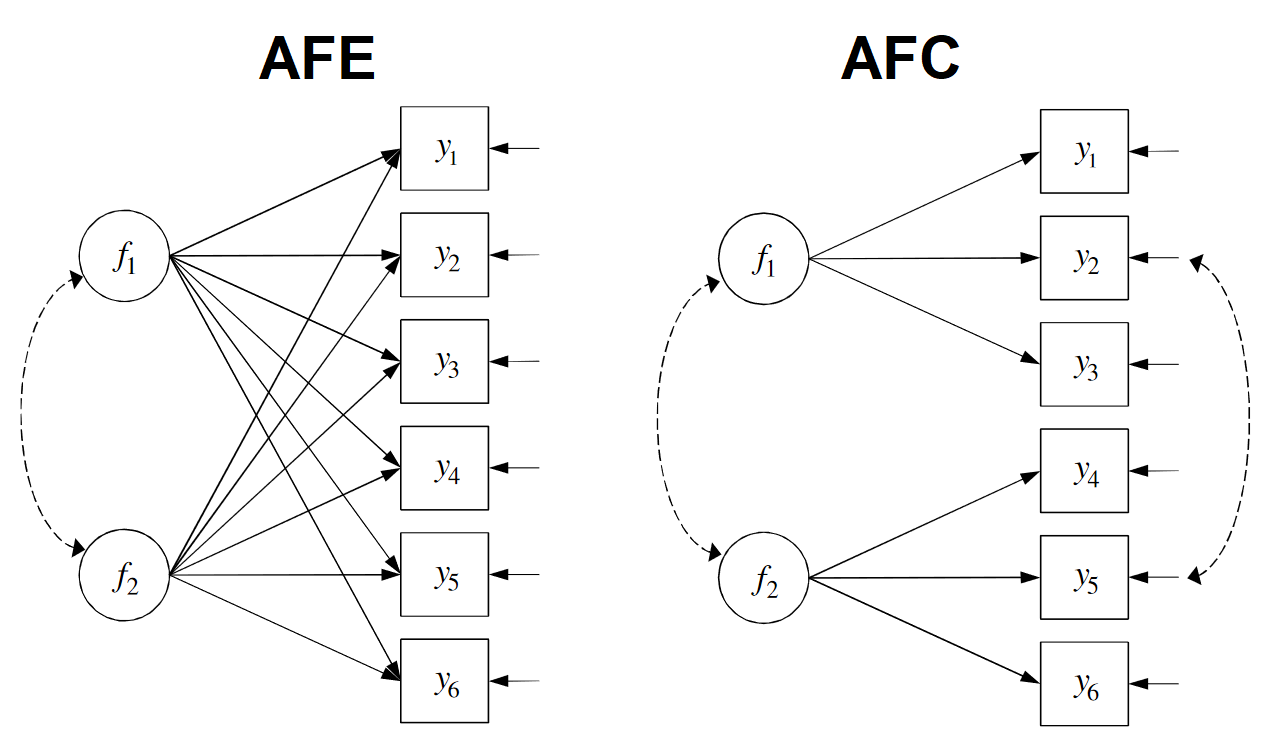
Figure B.2: Analyses en facteurs communs exploratoire (AFE) et confirmatoire (AFC)
inspiré de Juhel (2019)
L’AFC comporte plusieurs étapes. Il faut d’abord, comme dans l’AF exploratoire, sélectionner les variables et les individus. L’étape de spécification consiste à choisir un certain nombre de facteurs et à fixer à 0, éventuellement à contraindre à l’égalité, certains paramètres des matrices \(\Lambda\), \(\Phi\) et \(\Theta\), en s’assurant que le nombre de paramètres à estimer est inférieur ou égal au nombre de degrés de liberté du modèle, lui-même fonction du nombre d’éléments de la matrice de covariance des variables observées. Une fois ces restrictions spécifiées, le modèle est ajusté aux données en employant l’une ou l’autre des méthodes d’estimation offertes par des programmes de modélisation structurale, le plus souvent le maximum de vraisemblance (ML), de telle sorte que la matrice de covariance impliquée par le modèle \(\hat \Sigma = \hat{\Lambda} \hat{\Phi} \hat{\Lambda}’ + \hat {\Theta}\) reproduise le mieux possible la matrice de covariance de l’échantillon.
L’étape de rotation de \(\Lambda\) est ici impossible car elle conduirait à une modification des valeurs des saturations fixées à 0 lors de la spécification du modèle.
L’ajustement du modèle est ensuite évalué au niveau global et au niveau de l’estimation de chaque paramètre. L’ajustement global est mesuré avec un test du \(\chi^2\) du rapport de vraisemblance qui conduit au rejet du modèle lorsqu’il est significatif. L’évaluation de l’ajustement global prend également appui sur divers indices d’ajustement (le Goodness-of-FIt statistic, le Root Mean Square Error of Approximation, le Standardised Root Mean square Residual…). Des critères d’information (par exemple l’Akaike Information Criterion, le Bayesian Information Criterion, le Cross-Validation index…) peuvent aussi servir à comparer plusieurs alternatives plausibles du modèle.
Si l’ajustement du modèle est de bonne qualité, il est possible d’affirmer que la structure factorielle spécifiée est compatible avec les données sans pouvoir se prononcer pour autant sur l’existence d’autres modèles, non testés, également compatibles avec les données. Si l’ajustement du modèle n’est pas satisfaisant, la structure factorielle pré-spécifiée peut être rejetée avec certitude et l’analyse s’arrête dans une approche strictement confirmatoire. Mais en général, le modèle est à nouveau spécifié en fixant, contraignant à l’égalité ou libérant des paramètres sur la base d’arguments substantiels ou d’éléments empiriques comme les erreurs-types des estimations et les indices de modification (par exemple, en fixant à 0 les paramètres non statistiquement significatifs). Cette « mise à jour » du modèle est alors estimée et son ajustement évalué. Lorsque ces étapes sont répétées jusqu’à obtenir un ajustement acceptable, la différence entre l’AF exploratoire et l’AF confirmatoire s’estompe.
Ces dernières années, les modèles d’AFC ont été intégrés dans des modèles d’équations structurelles pour lesquels les facteurs sont régressés sur d’autres variables observées (« covariables externes »). Ces modèles MIMIC (multiple indicators multiple causes model ; Jöreskog & Goldberger (1975)) présentent l’avantage de permettre l’estimation de l’influence statistique de variables observées sur des facteurs sans avoir à calculer de scores factoriels.
B.3 Méthodes d’Analyses factorielles
B.3.1 Les différentes méthodes
B.3.1.1 Objectifs
Les techniques d’analyse factorielle ne supposent pas l’existence de variables latentes sous-jacentes aux variations et covariations observées et visent simplement à redistribuer la variance totale des variables observées en composantes afin d’opérer à une « réduction de données ».
Alors que l’Analyse en Composantes Principales (ACP, Hotelling (1933)) concerne des variables uniquement continues, l’Analyse Factorielle des Correspondances (Benzécri (1982)) permet d’analyser le lien entre deux variables discrètes. Concrètement, il s’agit de réaliser une ACP sur les profils lignes et colonnes du tableau de contingence en utilisant une distance du \(\chi^2\).
Enfin, l’ACM est une simple extension de l’aire d’applicabilité de l’Analyse Factorielle des Correspondances, en étendant le cas des tables de contingences à des « tableaux disjonctifs complet » (TDC) ou « tableaux de Burt » (TB) afin d’analyser plus de deux variables discrètes. Un exemple typique de ces données est celui des enquêtes d’opinion comme le Baromètre d’opinion de la Drees que nous mobilisons.
Comme pour l’ACP, l’ACM permet une représentation des individus en suivant des objectifs similaires (choix du nombre d’axes, interprétation, contribution, qualité…).
B.3.1.2 Formalisation mathématique
Soit un TDC concernant \(I\) individus décrits par \(J\) variables qualitatives, pouvant prendre en tout \(K\) modalités. Supposons que la première variable prend les modalités\(\{1,2,...,K_{1}\}\), que la deuxième variable prend les modalités \(\{K_{1}+1,K_{1}+2,...,K_{1}+K_{2}\}\) et ainsi de suite. Soient \(K=\sum _{j}K_{j}\) et \(\{1,2,...,K\}\) les \(K\) modalités possibles. On note \(X\) ce TDC à \(I\) lignes et \(K\) colonnes dans lequel, à l’intersection de la ligne \(i\) et de la colonne \(k\) (associée à la modalité \(k\)), on trouve :
- 1 si l’individu \(i\) possède la modalité \(k\) ;
- 0 sinon
Notons qu’il est possible d’inclure une variable quantitative dans l’analyse à condition de remplacer ses valeurs numériques en plage de valeur, afin de la convertir en variable catégorielle.
Le traitement mathématique du TDC \(X\) est le suivant : On calcule d’abord \(Z=X/(IK)\), puis le vecteur \(r\), qui contient la somme en ligne de la matrice \(Z\) et \(c\), qui contient la somme en colonne de la matrice \(Z\). On note également \(D_{r}={\text{diag}}(r)\) et \(D_{c}={\text{diag}}(c)\) les matrices diagonales issues de \(r\) et \(c\) respectivement. L’étape clé est une décomposition en valeurs singulières de la matrice suivante :
\[M=D_{r}^{-1/2}(Z-rc^{t})D_{c}^{-1/2}\]
La décomposition de \(M\) donne accès aux matrices \(P\), \(\Delta\) et \(Q\) telles que \(M=P\Delta Q^{t}\) avec \(P\), \(Q\) deux matrices unitaires et \(\Delta\) est la matrice diagonale généralisée contenant les valeurs singulières ordonnées de la plus grande à la plus petite. \(\Delta\) a les mêmes dimensions que \(Z\). Les coefficients diagonaux de \(\Delta ^{2}\) sont les valeurs propres de \(Z\) et correspondent à l’inertie de chacun des facteurs. Ces facteurs sont les coordonnées des individus (ligne) ou variables (colonne) sur chacun des axes factoriels. Les coordonnées des individus dans ce nouvel espace vectoriel sont données par la formule suivante :
\[F=D_{r}^{-1/2}P\Delta\]
La \(i\)-ième ligne de \(F\) contient les coordonnées du \(i\)-ième individu dans l’espace factoriel, tandis que les coordonnées des variables dans le même espace factoriel sont données par :
\[G=D_{c}^{-1/2}Q\Delta ^{t}\]
B.3.2 Effet Guttman
En analyse factorielle, il arrive parfois que le nuage projeté sur le premier plan factoriel ait une allure parabolique. Ce phénomène est appelé effet Guttman. Il révèle l’existence d’un premier axe associé à une valeur propre particulièrement élevée (épuisant à lui-seul une bonne partie de l’inertie totale du nuage) qui trie l’ensemble des variables selon une même échelle et signale une redondance entre les variables étudiées. Ce phénomène se présente souvent en ACM, en particulier en présence de variables au nombre de modalités impaire. L’axe principal oppose alors des situations extrêmes alors que le deuxième axe oppose les individus moyens à ces deux extrêmes.
Si cette situation se présente, il est possible (mais non assuré) de trouver du sens à l’interprétation des axes qui suivent. Lorsque l’effet Guttman est lié à la présence de modalités médianes dans les variables analysées, il est aussi possible de tenter de dichotomiser ces variables. D’autres méthodes de correction, telles que l’ « analyse des correspondances dédoublée » (Benzécri, 1980) existent mais posent des difficultés d’interprétation.
Joindre les points qui représentent l’effet Guttman permet d’examiner les « accidents » de la courbe, qui représentent une répartition originale par rapport à la norme.
B.3.3 Analyse Factorielle versus Analyse en facteurs communs
Même s’il y a souvent assimilation entre analyse factorielle et analyse en facteurs communs, ces deux notions sont pourtant très différentes : la première correspond à un modèle descriptif des données alors que la seconde est un modèle structurel.
Les méthodes d’analyse factorielle – ACP pour les variables quantitatives et son équivalent ACM pour les variables qualitatives – ont pour principal objectif la réduction de la dimension des données, c’est-à-dire construire de nouvelles variables, ordonnées par importance et résumant le plus d’information possible à partir des variables initiales. Dans ces méthodes, la variance unique est considérée inexistante et la variance commune devient alors la variance totale. Chaque variable est simplement mesurée comme une fonction linéaire des composantes principales et la structure des corrélations entre variables n’est pas nécessairement conservée.
À l’inverse, l’AF différencie variances commune et unique afin de chercher à identifier des facteurs latents. Elle cherche, contrairement aux méthodes d’analyse factorielle, à comprendre la structure des corrélations (termes non diagonaux de la matrice \(\Sigma\)) entre les variables mesurées dans la base de données et ne se focalise pas sur la variance (termes diagonaux). Les facteurs construits tiennent ainsi compte de la variance commune (plutôt que totale comme dans une analyse factorielle) et la corrélation entre deux variables dépend alors de la similarité de leur relation avec les facteurs latents.
Malgré ces différences, les méthodes d’analyse factorielle peuvent toutefois dans certains cas se substituer à l’analyse en facteurs communs. De nombreux articles, comme Velicer & Jackson (1990), indiquent même qu’il y a en pratique très peu de différences entre les deux approches dans la majeure partie des cas33 et que, même mathématiquement, ces méthodes sont voisines. Les méthodes d’analyse factorielle ont aussi comme gros avantage un fonctionnement computationnel simplifié car elles utilisent des méthodes d’estimation algébriques, plus simples que les méthodes types maximum de vraisemblance mobilisées en AF. Les méthodes d’AF se confrontent parfois aux « cas Heywood » (évoqués plus haut), c’est-à-dire des situations où les communautés des variables mesurées sont supérieures ou égales à 1 et faussent la modélisation (une variable ne peut pas résumer plus de 100 % de la variance).
Mais même si ces deux approches produisent parfois des résultats similaires, ce n’est pas le cas dans de nombreux contextes : quand les données contiennent des erreurs de mesure (rendues compte dans les AF mais pas en analyse factorielle), ou des valeurs extrêmes (non supportées en analyse factorielle). Par ailleurs, les modèles en facteurs communs peuvent être testés car supposent certaines hypothèses structurelles sur les données. Le modèle est rejeté s’il est mal estimé par les données, chose qui ne peut pas être faite avec des analyses factorielles.
Ce calcul suppose que la matrice de corrélation de la population est disponible.↩︎
L’avantage de l’estimation par maximum de vraisemblance est que cette méthode s’accompagne de nombreux indicateurs permettant de comparer la qualité de l’estimation du modèle et de mettre en place des tests de significativité et intervalles de confiance des saturations. Cette méthode repose toutefois sur une hypothèse de normalité multivariée. Pour ces raisons, il est parfois utile d’utiliser d’autres méthodes comme les principaux facteurs.↩︎
Alors qu’en ACP, appliquer une rotation change la solution↩︎
A ne pas confondre avec l’acronyme de l’« Analyse factorielle des correspondances », une autre méthode, cette fois-ci d’analyse factorielle, non utilisée ici.↩︎
On fixe à 0 les saturations des variables observées sur les facteurs dont elles ne sont pas des indicateurs. Les paramètres estimés sont dits libérés.↩︎
Pour rappel, dans l’expression de \(\Sigma\) en AFE, \(\Theta\) était remplacé par \(\Psi^2\) telle que \(\Psi [p, p]\) était la matrice diagonale des variances uniques des variables observées, l’AF confirmatoire accepte l’hypothèse d’erreurs corrélées, par exemple en cas d’erreurs de mesure.↩︎
Velicer & Jackson (1990) vont même plus loin en indiquant que les différences entre méthodes se font surtout sentir quand les modèles s’estiment mal, avec des saturations très faibles et que ces différences sont souvent en défaveur de l’AF.↩︎